Ideal Gas Law Definition
The ideal gases obey the ideal gas law perfectly. This law states that: the volume of a given amount of gas is directly proportional to the number on moles of gas, directly proportional to the temperature and inversely proportional to the pressure. i.e. pV = nRT.
The gas laws
The volume of any gas sample depends on the temperature and pressure applied to it. Any change in temperature and pressure will affect the volume. The laws that describes about the relationship between these three parameters of gas are know as gas laws. These laws are stated below:
Boyles law
Boyles law states that at constant temperature, the volume of a particular mass of gas is inversely proportional to its pressure. If the pressure is doubled, the volume is halved.
The mathematical expression of this law is
V∝ 1/P (where T and n are constant)
⇒ V = k X 1/P (where k is a proportionality constant)
⇒ PV = k
If P1 = the initial pressure of a gas, V1 = the initial volume of a gas.
And P2 = the final pressure of a gas, V2 = the final volume of a gas.
We can write,
P1V1 = k = P2V2
⇒ P1V1 = P2V2
Charles law
Charles law states that: at constant pressure, the volume of fixed mass of gas is directly proportional to the Kelvin temperature of absolute temperature. If the absolute temperature is double the volume is doubled.
Mathematically charles law can be expressed as:
V∝ T (where P and n are constant)
or V = kT (where k is a constant)
or V/T = k
If V1 = the initial volume of a gas, T1 = the initial temperature of that gas.
And V2 = the final volume of a gas, T2 = the final temperature of that gas.
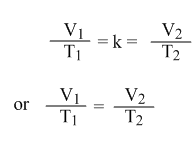
The combined gas law
Combining these two- Boyle’s and Charles’s law, we get
Boyle’s law V∝ 1/P (where T and n are constant)
Charles’s law V∝ T (where P and n are constant)
So we can write V∝ T/P (where n is constant)
Thus the combined law is: for a fixed mass of gas the volume is directly proportional to Kelvin temperature and inversely proportional to pressure.
If k is a proportionality constant,
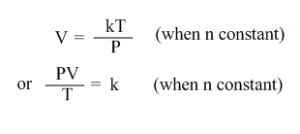
If P1 = the initial pressure of a gas, V1 = the initial volume of a gas, T1 = the initial temperature of that gas.
And P2 = the final pressure of a gas, V2 = the final volume of a gas, T2 = the final temperature of that gas.
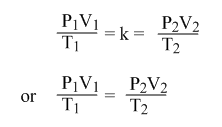
This equation can be used to solve any problem with a change in three variables P, V and T.
Avogadro’s law
Avogadro’s law stated that: Equal volume of gases at the same temperature and pressure contain equal number of moles or molecules. If the molar amount is doubled, the volume is doubled. So according to the law
V∝ n (where T and P constant)
or V = An (where A is the proportionality constant)
or V/n = A
If V1 = the initial volume of a gas, n1 = the initial moles of that gas.
And V2 = the final volume of a gas, n2 = the final moles of that gas.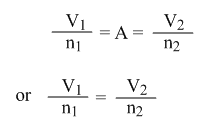
When V1 = V2, n1 = n2.
Derivation of PV = nRT
Combining these three laws- Boyle’s, Charles’s and Avogadro’s law, we get
Boyle’s law V∝ 1/P (where T and n are constant)
Charles’s law V∝ T (where P and n are constant)
Avogadro’s law V∝ n (where P and T are constant)
So combining these, we can write
V∝ nT/P
Thus the ideal gas law may be stated as: the volume of a given amount of gas is directly proportional to the number of moles of that gas, directly proportional to Kelvin temperature and inversely proportional to the pressure.
If R is a proportionality constant,
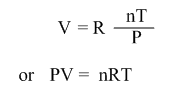
This is a ideal gas equation. This equation can be used to solve any problem with a change in three variables n, P, V and T.