Introduction of collision theory
According to this theory, a chemical reaction only takes place when two reacting molecules collide with sufficient kinetic energy. The reacting molecules collide with each other to perform a reaction. But not all the collisions are effective. When the reacting molecules collides with proper orientation and with sufficient kinetic energy, then a chemical reaction takes place.
Explanation
For productive collisions, the reacting molecules must:
- collide with proper orientation
- posses sufficient kinetic energy.
Collision with proper orientation
Let us consider a simple reaction where hydrogen and chlorine reacts to form hydrogen chloride gas.
H2 + Cl2 → 2HCl
A chemical reaction happens when the bond between two hydrogen atoms (H-H) or two oxygen atoms (Cl-Cl) breaks and a new bond forms between a hydrogen and chlorine atom (H-Cl). Before a productive collision the reacting molecules must posses sufficient kinetic energy. The collisions with less kinetic energy will be ineffective and will not perform any reaction to proceed. Thus the reacting molecules will simply bounce off from one another. The figure below shows the energy that a reacting molecules must posses to perform a reaction.
![Collision theory 5 By Community College Consortium for Bioscience Credentials (Own work) [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons](https://upload.wikimedia.org/wikipedia/commons/3/3a/Activation_Energy-c3bc.png)
The sufficient energy that is necessary for the reacting molecules to react with each other is known as activation energy (Ea).
Collision with proper orientation
A chemical reaction only happens when two reacting molecules collide with proper orientation. Proper orientation means in such a way that can lead to the breaking of existing bond and forming of the new bond.
Collision theory and reaction rate
Let us consider a simple reaction
A + B → C + D
Considering the postulates of collision theory, the rate of the reaction can be written as:
rate = f x p x z
Here f = fraction of molecules posses sufficient kinetic energy
p = probable fraction of effective collision
z = collision frequency.
Calculation of rate constant
The reaction rate increases with the increase of temperature. As for example: reaction rate doubles with an increase of temperature by 100c. Again kinetic energy of a gas increases with increase of temperature. That means, reacting molecules will acquire more kinetic energy to get over the energy barrier with the increase of temperature. So, we can say that when temperature increases, the kinetic energy increases and the reaction rate increases.
In 1989, Arhenius suggested a relation between the reaction rate and the temperature of a system.
k = A e-Ea/RT.
Here k = rate constant
A = an experimental value
Ea = activation energy
R = gas constant
T = Kelvin temperature.
Taking logarithm on each side of the Arhenius equation, we can write
\(\ln { k } =\quad -\frac { Ea }{ RT } \quad +\quad \ln { A } \)…………(i) \(\log { A } =\quad -\frac { Ea }{ 2.303 RT } \quad +\quad \log { A } \)
At temperature T1 and the rate constant k1,
\(\ln { { k }_{ 1 } } =\quad -\frac { Ea }{ R{ T }_{ 1 } } \quad +\quad \ln { A } \)………………….(ii)
At temperature T2 and the rate constant k2,
\(\ln { { k }_{ 2 } } =\quad -\frac { Ea }{ R{ T }_{ 2 } } \quad +\quad \ln { A } \)…………………(iii)
Subtracting the equation (ii) from (iii), we get
\(\ln { { k }_{ 2 } } -\quad \ln { { k }_{ 1 } } =\quad \left( -\frac { Ea }{ R{ T }_{ 2 } } \quad +\quad \ln { A } \right) \\ \quad \quad \quad \quad \quad \quad \quad -\quad \left( -\frac { Ea }{ R{ T }_{ 1 } } \quad +\quad \ln { A } \right) \\ \)
\(\ln { { k }_{ 2 } } -\quad \ln { { k }_{ 1 } } =\left( -\frac { Ea }{ R{ T }_{ 2 } } \quad +\quad \frac { Ea }{ R{ T }_{ 1 } } \right) \)
\(\ln { \frac { { k }_{ 2 } }{ { k }_{ 1 } } } =\quad \frac { { E }_{ a } }{ R } \left[ \frac { 1 }{ { T }_{ 1 } } -\frac { 1 }{ { T }_{ 2 } } \right] \)
\(\log { \frac { { k }_{ 2 } }{ { k }_{ 1 } } } =\quad \frac { { E }_{ a } }{ 2.303R } \left[ \frac { 1 }{ { T }_{ 1 } } -\frac { 1 }{ { T }_{ 2 } } \right] \)
From this equation the activation energy Ea can be calculated.
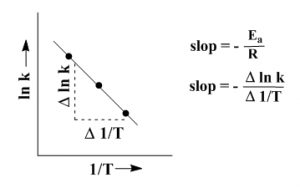
Calculation of Ea from a plot
Equation (ii) can be rewritten as
\(\ln { { k } } =\quad -\frac { Ea }{ R } \quad \left( -\frac { 1 }{ { T } } \right) +\quad \ln { A } \\ \quad \uparrow \quad \quad \quad \uparrow \quad \quad \quad \quad \quad \quad \quad \uparrow \\ \quad y\quad = mx\quad \quad \quad + \quad b\)…………….(iv)
The equation (iv) corresponds to the straight line equation y = mx + b. The two variables in this equation are ln k and 1/T. Plotting these two we get a straight line. From the slop of the line we can calculate Ea.
Limitations of collision theory
Although the collision theory of reaction rate is logical, but it has following limitations:
- The theory only applies to simple gases and sometime for solution where the reacting species are simple molecules.
- The expression from the collision theory (Arhenius equation) only applies to simple bimolecular reactions. For complex reactions the experimental value does not match with the calculated one.
- In this theory only kinetic energy of reacting molecules are considered, while the rotational and vibrational energy are ignored.