Definition
It is a quantitative relationship between temperature and volume of a gas. It was given by French scientist J. Charles in 1787.
According to this law, the volume of the given mass of a gas is directly proportional to the absolute temperature when the pressure is kept constant.
V α T (when pressure and number of moles are constant)
V = kT
V/T = k
If the temperature is changed from T1 to T2 and volume changes from V1 to V2, then
V 1/ T1 = k and V2 / T2 = k
So, V 1/ T1 = V2/ T2
V1 = initial volume
T1 = initial temperature
V2= final volume
T2 = final temperature
It can be written as
V2 = V1 (T2 / T1)
V2= final volume
T2 = final temperature
V1 = initial volume
T1 = initial temperature
The ratio of volume to temperature remains constant for same amount of gas at same pressure.
The law determines the linear relationship between volume and temperature. The temperatures are measured in Kelvin, which is SI unit of temperature.
Explanation
James Clerk Maxwell claimed that a space is occupied by a gas is dependent upon the motion of its particles. The particles continuously collide with the walls of the container. This rapid collision exerts force on the container surface, that force creates pressure.
The impact of this force is inconsequential but collectively the collision exerts pressure on the surface of the container. Gas pressure is proportional to the magnitude of collision and the force. So, the more collision results in higher pressure. However, it is also realized that the pressure is increasing with the increase in temperature provided the volume of the container kept constant. This behaviour is evident in the air pumps that churn out hot air when their piston is periodically pushed and pulled.
Volume increases in heated gas because volume isn’t bounded as ball expands pressure is also increases. The rubber expands as more hot gas is pumped in and the exhilarated particles bounce and push on the inside of the surface, pushing it outward. They obey Charles’s law [1].
Experimental Verification
Let us consider a certain amount of a gas enclosed in a cylinder fitted with a moveable piston. The volume of the gas is V1 and its temperature is T1. When the gas in the cylinder is heated both volume and the temperature of the gas increase. The new values of volume and temperature are V2 and T2 respectively.
Example
If 250 cm3 of hydrogen is cooled from 127oC to -27oC by maintaining the pressure constant. Calculate the new volume of the gas at low temperature.
Solution
Pressure has been kept constant so this gas is obeying the Charles’s law
Initial volume (V1) =250cm3 =0.25 dm3
Initial temperature (T1) = 127OC +273 K =400K
Final temperature (T2) = -27OC +273 K = 246 K
Final volume (V2) = Ɂ
According to Charles’s law
V 1/ T1 = V2/ T2
V2= V1 x T2 / T1
V2 = 0.25 dm3 x 246K /400K = 0.153 dm3 = 153 cm3 Answer
So, by decreasing the temperature the volume of the gas has decreased at constant temperature.
Graphical Explanation
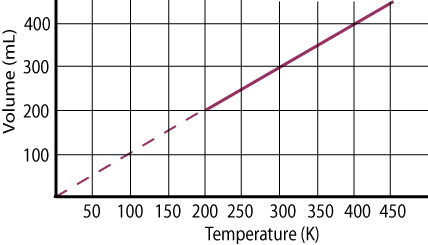
If we plot a graph between temperature on x-axis and the volume of one mole of an ideal gas on the y-axis, we get a straight line which cuts the temperature axis at -273.16o C. this can be possible only if we extrapolate the graph upto -273.16oC. This temperature is the lowest possible temperature which would have been achieved if the substance remains in the gaseous state. Actually, all the gases are converted into liquids above this temperature.
Charles‘s law is obeyed when the temperature is taken on Kelvin scale. For example, at 238 K (10O C) the volume is 566cm3 while at 373 K (100oC) the volume is 746 cm3. According to Charles’s law
V 1/ T1 = V2/T2 = k
566/283 = 746/373 =2= k
Greater the mass of gas taken, greater will be the slope of straight line. The reason is that greater the number of moles greater the volume occupied. All these straight lines when extrapolated meet at a single point of -273.16oC (0 Kelvin). It is apparent that this temperature of -273.16oC will be attained when the volume becomes zero. But for real gas the zero volume is impossible which shows that this temperature cannot be attained for a real gas. This is how we recognized that -273.16o C must represent the coldest temperature.
Relation to Absolute zero
According to Charles’s law gas will descend to zero at certain temperature. Gay- Lussac said that this law is not applicable at low temperature:
He said that compressed vapours remain entirely in their elastic state and they require temperature to enable them to resist the pressure.
At absolute zero temperature gas has zero energy so molecule restrict their motion Gay-Lussac also demonstrate that the Charles’s law doesn’t applicable just above the boiling point of the liquid. For example, ether is only a little above of its boiling point.
William Thomson was the first who mention that volume of a gas might descend to zero. He describe absolute zero in terms of the second law of thermodynamics.
Derivation of Absolute Zero
In order to derive absolute zero of temperature, consider the following quantitative definition of Charles’s law.
At constant pressure the volume of the given mass of the gas increases or decreases by 1\273 of its original volume at 0oC for every 1oC rise or fall in temperature respectively.
The general equation to know the volume of the gas at various temperature is
Vt= V0 (1+t\273)
Vt = volume of gas at temperature T
V0 = volume of gas at 0o C
t = temperature on centigrade or Celsius scale
if a gas is warmed by 1oC, it expands by 1\273 of its original volume at 00 C. Since original volume is 546cm3, so for 10 C rise in temperature 2cm3 increase in volume will take place. 2cm3 is the 1\273 of 546cm3. Similarly for 1000C rise in temperature, a change of 200cm3will take place.
For example, the increase in temperature from 100C to 1000 C, increase in volume from 566cm3 to 746cm3.
Relation to kinetic theory
The kinetic theory of gases is related to the macroscopic properties of gases like pressure and volume. It is also related to the microscopic properties of molecules like speed and mass of the molecules which make up the gas. In this theory temperature is taken as proportional to the average kinetic energy of the gas molecule.
T α Ek
Application
- Hot air balloons
`An object floats in a fluid when it weigh less than the fluid it displaces. According to Charles’s law, balloon is filled with heated gas, so volume expand. At elevated volume, the balloon occupies a greater volume in the same weight. Its density is lesser than the cold air so balloon begins to rise.
- Bloated tires
According to Charles law, the bloated tubes protruding out from a tire when we left in summer heat. The heat outside steadily enter into tubes and gradually causes the tire to expand. It is highly recommended to check your tires daily in summers. Because if subjected to further expansion the tires can burst at any second.
- Automobiles
In automobile engine series of pistons are lined up they are periodically bob up and down when there is presence or absence of fluid. The one end of piston is attached with crankshaft so rise or fall rotate the shaft and other end is attached with rear wheel of automobile. According to Charles’s law pistons are pushed by gas which is produced by fuel combustion. The combustion produce great amount of heat. So temperature rise and converted gas expands. They push them with force and thrust the vehicle forward.
Properties of Gases
- Gases don’t have a definite volume and occupy all the available space. The volume of a gas is the volume of the container.
- They don’t have a definite shape and take the shape of the container just like liquids.
- Due to low densities of gases, as compared to those of liquids and solids, the bubble through liquids and tend to rise up.
- Gases can diffuse and effuse.
- Gases can be compressed by applying a pressure because there are large empty spaces between their molecules.
- Gases can expands on heating.
- When sudden expansion of gases occurs cooling takes place, it is called Joule Thomson effect.
- Molecules of gases are in a constant state of random motion. They can exert a certain pressure on the walls of the container and this pressure is due to the number of collisions.
- The intermolecular forces in gases are very weak [3].
- Gases temperature is proportional to the average kinetic energy of the molecules.
The Ideal Gas Equation
According to Boyle’s law:
Vα 1/P
According to Charles’s law:
Vα T
It is well known fact that volume of the given gas at constant temperature and pressure is directly proportional to the number of moles (Avogadro’s law)
Vα n
So by these equations
Vα nT/P
V= constant nT/P
The constant is R which is called general gas constant.
V= R nT/P
Reference
- https://www.scienceabc.com/nature/universe/charles-law-definition-formula-equation.html
- https://en.wikipedia.org/wiki/Charles%27s_law
- https://www.chemguide.co.uk/physical/kt/idealgases.html